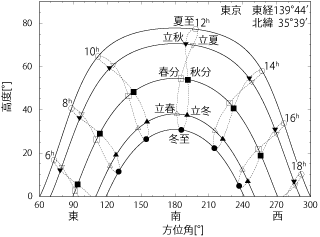
図は東京における1年間の太陽の高度と方位角.
記号は●:冬至,△:立春,□:春分,▽:立夏,
○:夏至,▼:立秋,■:秋分,▲:立冬を表す.
任意の地点における任意時刻の太陽の高度と方位角を年表掲載値を用いて計算する.
高度 h,方位角 A は
で求められる.
ここで δ は太陽の視赤緯,H は時角,φ は場所の緯度.t を高度・方位角を求める時刻−標準時 (日本の場合は9h) とし,λ を場所の経度 (東経を+,西経を−で表し,15で割って時間の単位にする),θ0 を世界時 0hのグリニジ視恒星時,α を太陽の視赤経とすれば,時角は H = θ0 + t × 1.0027379 + λ − α で求められる.もし,H が負になれば 24h を加え,24h を超えれば 24h を引く.年表に掲載されているα, δ は世界時 0h の値なので,式に代入するためには時刻 t の値を求めなければならない.高度・方位角を度の桁まで求めるのであれば,α, δ の値は当日と翌日の間の比例配分で求めてよい.また,大気差の影響も無視してよい.方位角は式(1)と式(2)から求める.もし,式(2)が−の場合は A に180°を加え,式(1)が−で式(2)が+の場合は A に360°を加える.測る方向は北から東,南,西まわりとなる.高度は式(3)から求める.
影の長さは影をつくる物体の高さ × cot h で,影の方位角は太陽の方位角に180°を加えて求める (360°を超えた場合 360°を引く).
東京における2005年12月22日12時の太陽の高度と方位角を求める.東京の経度と緯度を地図から読み取る.東経 λ = +139°44′= +9h18.9m,北緯 φ = 35°39′,sin φ = 0.58283,cos φ = 0.81259を得る.12月22日のグリニジ視恒星時 θ0 = 6h2.6m (年表:世界時0hのグリニジ視恒星時のページ参照),22日と23日の太陽の視赤経α0 = 18h1.0m と α1 = 18h5.4m,視赤緯δ0 = −23°26.4′と δ1 = −23°26.1′(年表:太陽,月のページ参照) を求める.
高度・方位角を求める時刻 (世界時) t = 12 − 9 = 3h,この時刻の太陽の視赤経,視赤緯は
α = (α1 − α0) × 3 / 24 + α0 = (18h5.4m − 18h1.0m) × 3 / 24 + 18h1.0m = 18h1.6m
δ = (δ1 − δ0) × 3 / 24 + δ0 = {−23°26.1′ − (−23°26.4′)} × 3 / 24 + (−23°26.4′) = −23°26.4′
となり,cos δ = 0.91748,sin δ = −0.39779 が求まる.
太陽の時角 H = 6h2.6m + (12 − 9)h × 1.0027379 + 9h18.9m − 18h1.6m = 20.5m (= 5.1°) となる.
式(1)と式(2)を計算すると,cos h sin A = −0.081829,cos h cos A = −0.85584.ここから,A = arctan (−0.081829 / −0.85584) = 5.5°,式(2)が−だから A に180°を加えて方位角 A = 185.5°を得る.式(3)を計算し,sin h = 0.51072から,高度 h = 30.7°を得る.
このとき垂直に立てた1メートルの棒の影の長さは 1 × cot h = 1.7メートルとなり,影の方向は A + 180°= 365.5°となる.360°を超えるので360°を引いて5.5°を得る.
なお,表記の値は紙面の都合上四捨五入されているが,実際の計算は有効桁による.
暦象年表2005より加筆、訂正