国民の祝日に関する法律では,秋分の日は秋分日となっており,具体的な日付が記されていない.ここでいう秋分日とは二十四節気の秋分を含む日,つまり太陽が秋分点を通過する日のことである.このような定義の仕方は秋季皇霊祭が休暇日に定められた明治11年(1878)6月5日 太政官達第23号のころから変わっていない.
変わっていないといえば,秋分の日は長らく9月23日のままであった.平成24年(2012),これがついに9月22日となる.9月23日でなくなるのは昭和54年(1979)9月24日以来33年ぶり,9月22日になるのは明治29年(1896)以来116年ぶりの出来事である.今回はこのあたりの背景について考えてみよう.

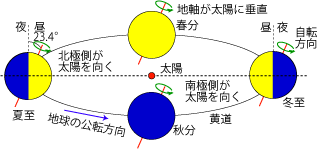
地球は1年かけて太陽の周りをまわっている (図1).地球の自転軸は地球の運動面に対して垂直ではないから,北極側が太陽を向く時期と逆を向く時期が存在することになる.北半球においては前者が夏で後者が冬,その中間は春や秋となり,地球が軌道上のどこにいるかによって季節は定まる.この軌道上の位置をより細分化したものが二十四節気であり,とくに先の4点はそれぞれ夏至,冬至,春分,秋分と呼ばれている.1年=365日と思っている人もいるだろうが,この地球の運動=季節のめぐりこそが,真の1年=1太陽年≈365.2422日=365日+6時間弱なのである.
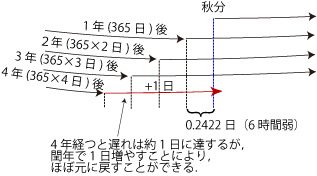
この,6時間弱という端数のために秋分点通過時刻は年々遅くなっていく (図2).といっても,4年経つとその累計はほぼ1日になるから,4年おきに1日増やす,つまり閏年を作ることでだいたい元の状態に戻すことができる.このように,季節と日付が大きくずれていかないようにすることが閏年を設ける理由であり,このような暦をユリウス暦という.ユリウス暦の1年の長さは平均365.25日になる.
このとき日付がどうなるか,少し具体的な時刻を使って考えてみよう.はじめに秋分点を通過する時刻が10時だとすると (表1の例1),通過時刻が遅くなる過程で秋分の日の日付も変わることがわかる.だが,2時だとすると (例2),日付は変わらない.秋分の日はこれまで長い間,例2のような状態にあったわけである.
| 年 | 通過時刻 | 秋分の日 |
|---|---|---|
| はじめ | 23日10時 | 23日 |
| 1年後 | 23日16時ごろ | 23日 |
| 2年後 | 23日22時ごろ | 23日 |
| 3年後 | 24日04時ごろ | 24日 |
| 4年後 | 24日10時ごろ? | |
| →23日10時ごろ | 23日 |
| 年 | 通過時刻 | 秋分の日 |
|---|---|---|
| はじめ | 23日02時 | 23日 |
| 1年後 | 23日08時ごろ | 23日 |
| 2年後 | 23日14時ごろ | 23日 |
| 3年後 | 23日20時ごろ | 23日 |
| 4年後 | 24日02時ごろ? | |
| →23日02時ごろ | 23日 |
一方,0.2422 × 4 = 0.9688 だから,4年に1日の割合だと1 − 0.9688 = 0.0312日 ≈ 45分 だけ補正しすぎることになる.このため,4年後の通過時刻は逆に約45分ずつ早くなっていくのだ.平成24年の秋分の日が22日のように早くなるのもこれが原因である.
過剰な補正量は400年で3日に達するから,その分だけ閏年を減らすほうが長期的なずれは少なくて済む.そこまで考慮して定められた暦が現在も使われているグレゴリオ暦であり,この場合の1年の長さは平均365.2425日となる.
| 条件 | ユリウス暦 | グレゴリオ暦 | 例 |
|---|---|---|---|
| 西暦が4で割り切れる年 | 閏年 | 閏年 | 2004年,2008年,2012年 |
| うち100で割り切れる年 | 閏年 | 平年 | 1700年,1800年,1900年 |
| うち400で割り切れる年 | 閏年 | 閏年 | 1600年,2000年 |
実際に年ごとの秋分の時刻をグラフに表すと,図3のようになる.なお,本トピックスでは,説明を簡略化するために1太陽年≈365.2422日等の平均値を用いたが,秋分など二十四節気は地球から見た太陽が特定の位置にくる瞬間,たとえば秋分の場合は太陽の視黄経が180°になる瞬間の中央標準時として定義されるものであり,厳密には章動や月・惑星の影響,地球自転の変動なども考慮に入れる必要がある.
それでも,平年では1年あたり6時間弱ずつ遅れ,閏年になると4年前よりも少し前に戻る様子は十分に見て取れると思う.また,当分は4年おきに秋分の日が9月22日になること,しだいに9月22日となる割合が増えていくことなどもわかるだろう.
暦象年表2012より